Sorting algorithms, with visualizations and complexity comparisons published 12/5/2019 | 9 min read

Welcome everyone to a new story on devspedia. Today I'll showcase 8 sorting algorithms in JavaScript, with examples and complexity comparisons.

Let's get straight to it. Below is a list of these sorting techniques:

  1. Bubble Sort
  2. Selection Sort
  3. Insertion Sort
  4. Heap Sort
  5. Merge Sort
  6. Quicksort
  7. Shellsort
  8. Radix Sort


Bubble Sort:

Bubble Sort

Bubble sort works basically by iterating through the list while comparing list each adjacent pair of items in the list. If the order of these 2 items is invalid (based on whether you're sorting ascending or descending) then it swaps them.

It keeps repeating this same pattern over and over again until no extra swapping is necessary.

Complexity:



Selection Sort:

Selection Sort

Selection sort is has significant time complexity O(n2) which makes it very slow for large lists. Selection sort works by doing in-place comparison, so it'll iterate through all items and compare them 1 to 1, then start over. It keeps repeating again no more replacing is necessary.

Selection sort is similar to insertion sort, however it performs worse.  But in some scenarios selection sort can perform well in low memory systems, and with smaller lists.

Complexity:



Insertion Sort:

Insertion Sort

Insertion sort is — similar to previous selection sort — takes on item at a time too, it compares one item with it takes first item to the left, and compare it with the next item, then second item, and put before or after first item, then third item and compare it with second then first item and keep repeating this until all list is sorted.

Complexity:



Heap Sort:

Heap sort (using max heap)

Heap sort performs also runs on comparisons, but it's more efficient than selection or insertion sort because with every iteration it shrinks down the sortable scope of the list, resulting in fewer iterations until list is fully sorted.

It works by creating a max (or min) heap, and then take the top item of the heap tree and put it in the far right (if max heap) or far left (if min heap), and consider that number sorted, and then work only on the remaining items.

Complexity:

Merge Sort:

Merge Sort

Merge sort is a divide and conquer algorithm. Merge sort works by splitting the list into halves, and further until each group is only at most 2 items. Then it keep merging and growing up again to the full length of the list.

The steps for sorting will be by splitting them into smaller groups, compare groups together, then merge sorted items to a bigger group, then compare, then merge, and keep repeating until all items are sorted.

Complexity:

Quick Sort:

Quick sort

Quicksort is also a divide and conquer algorithm. It works by dividing the list into two smaller groups: group with lowest elements, and group with highest elements. It knows the lowest and highest elements by picking an item from the middle off the list, and grouping smaller values in 1 group, and higher values in another. Then quicksort can then recursively sort the the smaller groups by repeating the same steps.

Complexity:

Shell sort:

Shell sort

Quick sort is another in-place comparison sort algorithm. It works by sorting pairs of elements far apart from each other using an interval value for this distance that decreases while iterating, then progressively reducing the gap between elements to be compared. Starting with far apart elements, it can move some out-of-place elements into position faster than a simple nearest neighbor swap.

Check the following graphs for better explanation:

Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {(35,14)}, {(33, 19)}, {(42, 27)} and {(10, 44)}

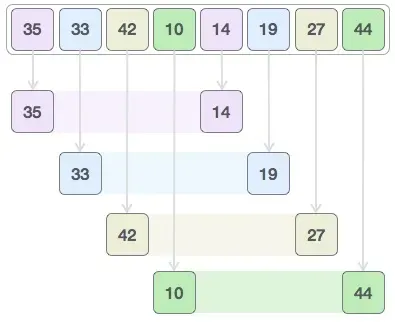
We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this:

Then, we take interval of 1 and this gap generates two sub-lists - {(14, 27, 35, 42)}, {(19, 10, 33, 44)}

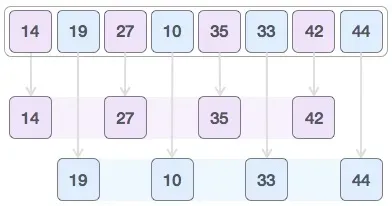
We compare and swap the values, if required, in the original array. After this step, the array should look like this:

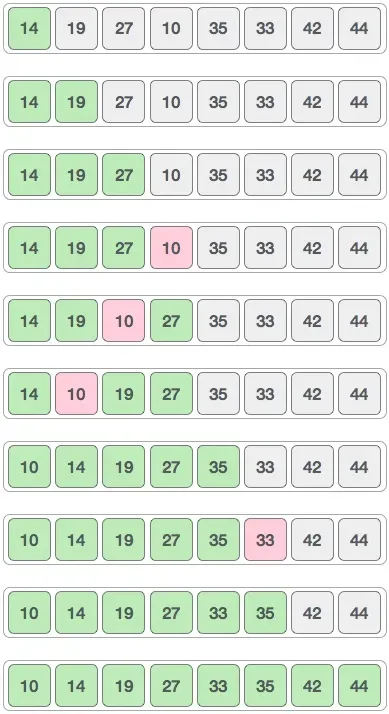
Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.

Following is the step-by-step depiction:

Complexity:

Radix Sort:

Radix Sort

Radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys by the individual digits which share the same significant position and value. A positional notation is required, but because integers can represent strings of characters (e.g., names or dates) and specially formatted floating point numbers, radix sort is not limited to integers.

What does Radix mean?

In mathematical numeral systems, the radix or base is the number of unique digits, including the digit zero, used to represent numbers in a positional numeral system. For example, a binary system (using numbers 0 and 1) has a radix of 2 and a decimal system (using numbers 0 to 9) has a radix of 10.

Complexity: (k means the longest key)

Resources:

Thanks for reading devspedia, I love you, and see you the next time :)



You may also like reading: